
For example, if you are studying the MPG of a car at various speeds, collect the same amount of data points for each interval of speed. Each measurement is taken as time progresses and can have its own set of circumstances.Įach subgroup contains data of a similar short term setting (one lot, one shift, one operator).Įasier analysis of subgroup data is done when the amounts of measurements per subgroup are equal.
#MINITAB I MR CHART FREE#
Determine whether the data is in INDIVIDUALS or SUBGROUPS.Įach measurement is free from a rational subgrouping. The three charts above are used when plotting continuous data. Furthermore, the range of each subgroup in 4-9 was exactly 1.0. In other words the range from subgroups in data point 1,2,3, and 10 was 2.0 exactly. It is not likely a natural process will perform exactly this consistently. The range chart points to the possibility that not enough decimals were used or more resolution should have been documented. However, since there are failed tests in the Xbar chart, there is a nonrandom or special cause variation present within the process and require additional investigation.Ī possible problem is the lack of measurement discrimination (aka granularity or resolution). The R chart is in control and therefore the control limits on the Xbar chart are accurate and an assessment can be made on the process center. The following process can not be assessed for capability. There are Nelson Tests, Western Electric Tests and often times you can adjust them to create your own conditions to test for process control. Some conditions of special cause can occur within the LCL and UCL (control limits). Recall, that not all out of control conditions are this obvious. Each of the 10 data points has 5 observations within it.
#MINITAB I MR CHART SOFTWARE#
Statistical software will normally have the ability to test for conditions that indicate process control or the lack thereof.Įach data point is the mean of a subgroup of 5 observations. The Xbar chart below shows an out of control process. Each data point has >1 observation record and this helps to identify true anomalies or capture a longer term representation of each data point. Xbar-R charts are recommended over I-MR charts primarily due to containing more data (which strengthens a decision). The R chart plots the range of the subgroups and is applied to assess whether the variation from subgroup to subgroup is in control. The I-MR chart obviously only has one observation point for each "group", or data point, so the plot is each point itself. The Xbar chart plots the mean of the each subgroup.
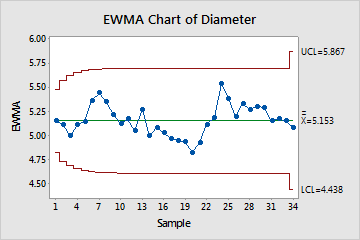
These charts are used to verify process control before assessing capability such as Cpk, Ppk, Cp, Pp, or Cpm. There are a few commonly used charts to assess process control If the R chart is out of control, then the control limits on the X-bar chart may be inaccurate and exhibit Type I or II error. The R chart is used to review the process variation which must be in control to correctly interpret the Xbar chart. The control limits of the Xbar chart are calculated with the inputs of the process spread and mean. This control chart, along with I-MR and X-bar & S, are used in measuring statistical process control and assessing the stability of a process. 2023.Īll rights reserved.Xbar R charts are often used collectively to plot the process mean (Xbar) and process range (R) over time for continuous data.
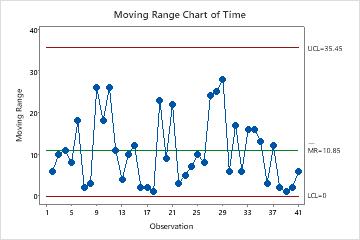
Displaying stratification in a control chart.Applying rules to a Shewhart control chart.Therefore an I-chart is often combined with an MR-chart to monitor process variability, although some authors question the benefit of an additional MR-chart. It is important to ensure process variability is in a state of statistical control before using the I-chart to investigate if the process mean is in control. If the process shows a moderate departure from normality, it may be preferable to transform the variable so that it is approximately normally distributed.
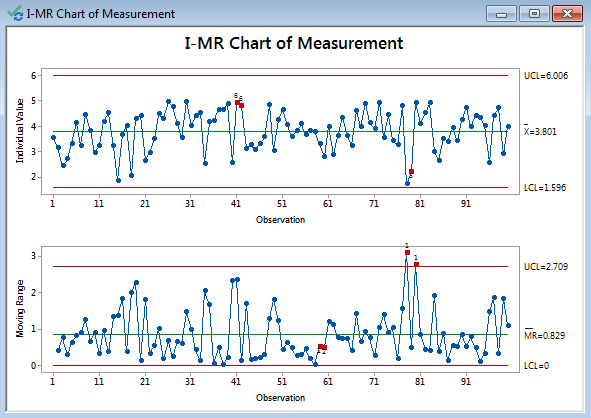
The observations are assumed to be independent and normally distributed. For a process with special causes of variation, both estimators are biased, and it may be preferable to use the median moving range estimator. For an in-control process, both estimators are unbiased, and the standard deviation is a more efficient estimator. If unspecified, the process sigma is the standard deviation of the individual observations, unless the chart is combined with an MR-chart where it is estimated as described for the respective chart.
A multiple (k) of sigma above and below the center line.


 0 kommentar(er)
0 kommentar(er)
